Conway's Game of Life on GPU using CUDA

I was quite satisfied with 140x speedup of the basic GPU implementation over the serial CPU but I decided to boost GPU's ego even further by hopefully faster implementation. Actually – two implementations. This chapter explains an easier one, next Chapter 4 Advanced lookup table implementation talks about more complicated one.

Every life cell has two states (alive or dead) which were so far represented as integers 1 and 0. I asked myself a question:

Usage of 1 bit per cell could be potentially more efficient and it could also cut memory requirements 8-times. So how to speed up cell state evaluation? The obvious way is to get rid of the summing part that is slow because it has too many memory reads — 8 memory reads per cell to be exact. If a life cell would be stored in one bit, a single read of a byte would actually read 8 cells. Even further, a single read of unsigned int (uint) retrieves 32 cells at once.

The idea of bit per cell sounds promising, but there is a little catch. Cells in one uint are in a row, but area of 3x3 cells is needed in order to evaluate a single cell. This means that three rows are needed, but it is still better than 9 memory reads.

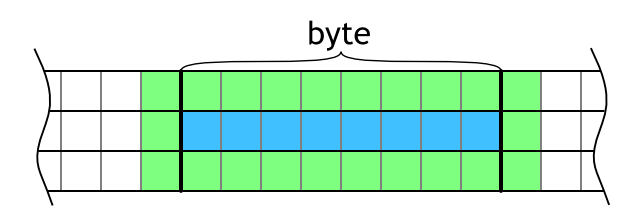
The goal is to evaluate whole byte of data (8 cells). It is necessary to load three rows and then it is possible to evaluate the middle row cell by cell by counting the number of living cells. The problem is that the neighborhood area overlaps to bytes before and after the current block as shown in Figure 1. This adds quite large overhead. Instead of reading 3 bytes and evaluating 1 byte, 9 bytes need to be read.

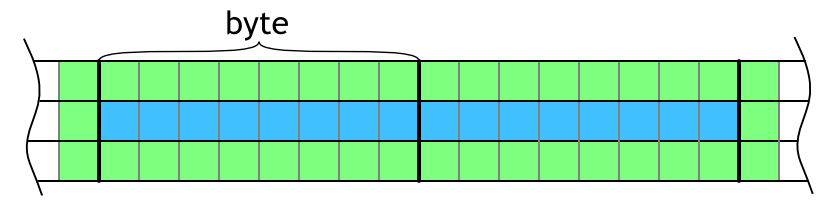
This overhead can be significantly reduced by evaluating more consecutive block in the row as shown in Figure 2. Actually, the overhead is constant — 2×3 bytes — no matter how many blocks are evaluated in between them. This means that the more bytes evaluated in the row, the better. However, more blocks in the row means more work per thread and too much work per thread can stall the GPU which is not good.

It is hard to guess what is the magical number of consecutive processed blocks (bytes) that would result in the best performance; I will leave this as a parameter of the method.

Code listing 1 shows the CUDA kernel. It is quite lengthy but I will try to describe it in detail in following paragraphs.

The kernel starts with a scary-looking for-cycle. Similarly as in previous Section 2.4 Simple GPU implementation, this cycle ensures that if the kernel is invoked with less threads then cells to process, every thread will loop through more cells to compute all of them.

The first thing computed in the main cycle is x and y coordinates based on given cell ID. All y coordinates are pre-multiplied with data width to avoid unnecessary multiplications later. This is necessary since the data are stored in 1D array and every y index has to skip whole row (data width).

Then, variables called data0, data1, and data2 are initialized with first two bytes of data. Those 4-byte (32-bit) integer variables represent rows of data and they are used to store three consecutive bytes of data to allow easy evaluation of the middle byte.

Next follows the for-cycle that goes over consecutively evaluated bytes. This concept was explained in previous Section 3.1 Evaluation of the cells. At the beginning of the cycle, a new byte is pushed to the datan variables by left-shifting existing content by 8 and or-ing new byte.

Then, another cycle goes over 8 cells that are evaluated. At every position, number of living cells is counted by some (clever) bit operations and based on the sum the result bit is written. Feel free to grab a piece of paper and sketch the bit operations to see what is happening. Basically, it is parallel bit summing on two positions and then summing to the final number.

A CPU implementation of the bit counting algorithm is nearly identical to the GPU implementation. The implementation is parallel and I did not even investigate a serial version of it. If you are interested in actual implementation details please see the code on GitHub.

The performance of the CPU version was evaluated for wide range of consecutive evaluated blocks (cb). The evaluation speeds are shown in Figure 3. The basic serial and parallel algorithms are shown in the figure for comparison.

Figure 3 clearly shows that the bit-per-cell algorithm is much faster than the basic one saving not only memory but speeding the evaluation as well. As expected, the more consecutive evaluated blocks (cb) the better. This is not the case for GPU as you can see in the next section.

GPU performance charts are a little harder to produce because there are two parameters that could vary: number of consecutive evaluated blocks and threads per CUDA block. The benchmark was run for all combinations of those two parameters the best for each of them was reported.

The best performance among threads per CUDA block was for value 128. Figure 4 shows evaluations speeds different values of consecutive evaluated blocks (cb) compared to the basic GPU implementation described in Chapter 2 Basic implementation. For the most values of cb the evaluation speed higher than the basic GPU implementation. However, the trend that more cb results in better performance as observed in the CPU implementation is not true now. The best value of cb is probably 8, for higher values the performance decreases and for 128 cb the evaluation speed is even lower than for the basic implementation.

For the completeness of the GPU implementation performance evaluation, Figure 5 shows the evaluation speed for different values of threads per CUDA block (tpb). The variance in results in not that big, the only outlier is the lowest value 32 tpb.

This chart nicely shows the speedup of the bit counting implementation over the basic GPU implementation which is about 2.5×. That is more than speedup for the CPU implementation which was about 2×.

Next section compares performance of best performing settings of the CPU and GPU algorithms.

For the final comparison of this chapter, the best performing settings were selected for the CPU and GPU. The CPU algorithm performed the best for 128 consecutive evaluated blocks (cb) and the GPU algorithm for 8 cb 128 threads per CUDA block (tpb). Section 3.5 CPU vs. GPU shows speedup of those two measurements and compares them with the basic parallel CPU and basic GPU for 128 tbp.

It is nicely visible that even the improved bit-per-cell CPU implementation is way slower than the basic GPU implementation. The improved GPU implementation is reaching speedups up to 480× over the basic serial CPU implementation.

But I will not stop here. As suggested in introduction of this chapter, reading of larger memory blocks might be more effective. Most hardware is optimized to read larger memory block as opposed to small ones. The idea is to read and write 32-bit words instead of 8-bit bytes.

The implementation has to be substantially changed in order to achieve this improvement. First, three consecutive blocks cannot be accumulated in one variable anymore.

Second, the CPU and GPU is using little endian for representing longer words than a byte. However, little endian stores the bytes in reversed order and it is not possible to process them sequentially. This problem is solved by swapping endianness while reading and writing.

The GPU implementation is shown in Code listing 2 and it is much longer than previous implementation. This is mainly due to overlaps that are handled separately to save memory and computations.

The implementation on CPU is again very similar to the CUDA kernel and uses Concurrency::parallel_for for parallelization.

Long story short, the promise of some speedup did not happen. Figure 7 shows speedup of the bit counting algorithm on big chunks for the CPU over the previous implementation of bit counting on smaller chunks. For any value of cb the speedup is lower than one. The situation is the same for the GPU, no speedup over the previous implementation as shown in Figure 8.

First, I was quite surprised by this result but then I realized that the overhead of reading small chunks is completely negated by caches.

I think that the lower performance is caused by overhead of dealing with large chunks (endianness switching, etc.). The algorithm for smaller chunks is actually faster. Thanks, caches!