Maraytr - Marek's Ray-tracer
5 Extensions
The basic ray-tracer was described in previous chapters. In this chapter I will go over some extra features. I might add new sections over time as new features will be implemented. If you would like to see some ray-tracer feature implemented then let me know down in the comments or send me an email.
5.1 CSG operations
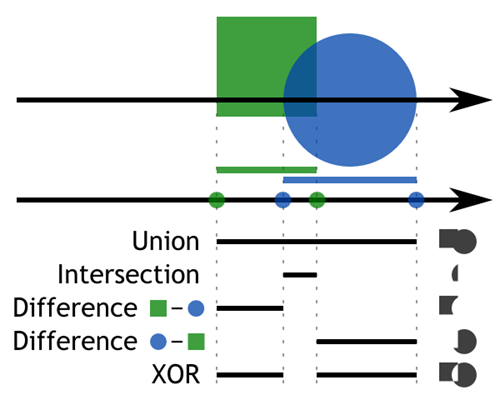
The cool part about CSG representation is ability to do boolean operations. The basic idea is to collect intersections from all children and filter them based on the boolean operation. I will describe here only union and intersection, others are similar. Figure 1 shows the process visually.
Note that in order to perform boolean operations correctly all intersections has to be paired. For every enter intersection has to be another exit intersection. This is why we ignored tangent intersection with the sphere in Section 2.2 CSG primitives. This may be tricky to fulfill with objects like half-space tha have only one intersection. I solve it by adding extra intersection that is in infinity.
The magic happens in the Intersect method of CsgBoolOperationNode. All intersections are collected to a list which is then sorted by the ray parameter. Now we have a list of intersections that comes how they appear among the ray. We will go through them one by one and produce new pruned list of intersections based on a boolean operation of the node.
For union, at least one object has to be present. For intersection all child object have to be present. We will keep track of number of objects we are currently in. Every enter intersection will increase the counter and every leave intersection will decrease it.
Now for the union, when counter increases from zero to one we save that intersection. If counter decreases from one to zero we again save the intersection. All other intersections will be not saved to the final list.
Intersection works the same but the reporting threshold is not one but n which is the number of children. Code listing 1 shows the code that performs described operation. The parameter requiredObjectsCount is one for union and n for intersection. This method can perform partial intersection where say only two overlapping objects are needed to satisfy intersection condition. I can imagine this partial intersection be used when having a long chain of spheres and every two are overlapping a little bit.
Code listing 1: Computation of union and intersection.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | int computeIntersection(List<Intersection> intersections, ICollection<Intersection> outIntersections, int requiredObjectsCount) { int insideCount = 0; int count = 0; foreach (var intersec in intersections) { if (intersec.IsEnter) { ++insideCount; if (insideCount == requiredObjectsCount) { outIntersections.Add(intersec); // Add entering intersection to the result. ++count; } } else { if (insideCount == requiredObjectsCount) { outIntersections.Add(intersec); // Add leaving intersection to the result. ++count; } --insideCount; } } Debug.Assert(insideCount == 0); return count; } |
I have created simple dice as an example of boolean operations (see Figure 2). The basic shape is an intersection of cube and sphere. Then corers are cut using cubes of size little smaller than diagonal of the main cube. Finally, small black spheres are used to cut the holes using subtraction operation.
This scene does not use ambient light. The shadowed are on the right side of the dice is lit by very soft blue-ish point light. If you look carefully you can see a shadow from it on the left side.